总结学习视频 https://www.bilibili.com/video/av94067702/

所有的优化器都是可以套进这个基本框架的。

这里的E指的是单位矩阵。SGD 没有动量概念，因为一阶动量就是当前梯度，二阶梯度就是单位矩阵。

缺点：容易陷入局部最优。由于SGD只考虑当前时刻的梯度，在局部最优点的当前梯度为0。由计算公式可知，此时参数不再进行更新，故陷入局部最优的状态。

显而易见，引入历史梯度值，引入动量（momentum）的概念可以帮助我们跳出鞍点。

咱比如要算 ${\theta }_t$ 的平均，一般大家就用相加求和/总数的方法。
而EMA（指数滑动平均）是指数式的平均。

第一行最重要，方便理解。
当前时刻 $v_t$ 等于 衰减因子$\beta$ 与上一个时刻的值 $v_{t?1}$ 的乘积 加上 $(1?\beta )\times {\theta }_t$。这个式子可以递归化简为第二行，也就是把${\theta }_t$的历史做一个指数的求和，所以很形象的称为滑动平均。

而对于那些权重小于 $\frac{1}{e}$的项，我们可以忽略不记。然后可以数学推导（极限），指数滑动平均肯定有个范围啊，就是到底与多宽的历史时刻有关，答案是 $\frac{1}{1?\beta }$，所以一般$\beta =0.999$的时候，就是1000个时刻取指数平均。

此时，我们知道了EMA，就可以把 ${\theta }_t$换成$g_t$，目的是引入梯度的历史值，进而可以计算出梯度的动量（momentum）。

当t比较小的时候，EMA会把平均值拉的很小。

所以这里大家一般都会引入一个修正因子$1?{\beta }^t$，我们可以分析，

在SGD上，加入一阶动量，还是没有引入二阶动量。

这里没有严格使用EMA，具体为，没有使用$1?{\beta }^t$，而是使用了 $\eta$，无伤大雅，原理上一致。

同样使用了一阶动量而没有使用二阶动量。没有使用 $(1?\beta )\times g_t$，而是预测t-1时刻下一时刻梯度，没有引入当前的观测值，可以理解为跟着惯性走了一步。

---

加下来的都是引入二阶后的方法。二阶动量出现，才说明了自适应学习率的优化算法时代到来。

如图，我们希望经常被刺激到的神经元参数更新幅度小一些，那些不经常被用到的神经元更新的慢一点。

有一种归一化的感觉。对于那些更新幅度很大的参数，通常历史累计梯度的平方和会很大（可以理解为能量很大），所以希望能量大的更新慢一点，能量小的更新快一点。

所以，如图式一，计算以往梯度的平方和作为二阶动量，梯度本身作为一阶动量，就可以得到第二行的式子。此时，二阶动量大的参数就会更新的小一点啦。

缺点：随着时间步的拉长，历史累计梯度平方和会越来越大，这样会使得所有维度参数的学习率都不断减小（单调递减），无论更新幅度如何。

显然，一直累计肯定不好，这里可以想到momentum，利用EMA不就好了吗？

Delta 就是一个小范围嘛，就是使用了历史一部分梯度。

• RMSProp 就是在AdaGrad 基础上将普通的历史累计梯度平方和换成了历史累计梯度平方和的EMA
  

• AdaDelta
  在 RMSProp上进行，改的分子（忽略）

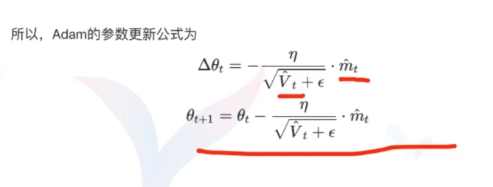
Momentum 在SGD 基础上增加了一阶动量，AdaGrad 在SGD 基础上增加了二阶动量， 把一阶和二阶动量都使用了就是Adam。