
18888889999
notice 网站公告
— 杏彩体育资讯 —
这几年的学习中,我偶尔会碰到一些比较复杂的、变量比较多的最优化求解问题;简单的最优化求解问题当然可以套用运筹学或凸优化的一些方法,但是往往很多问题是无法求出解析解的,只能用一些数值方法作近似求解;我觉得有必要总结一下自己的学习历程,以便日后查看。
最著名的数值优化方法当然是一系列的智能算法,以及因为近年机器学习的兴起而带动发展起来的、专门用于减轻调参难度的贝叶斯优化方法。本文会根据我自己的经验和认识总结一下四种算法:遗传算法、粒子群算法、模拟退火算法和贝叶斯优化。
数值最优化方法本质是用一些迭代算法去找到整个函数或一些实际问题的近似可能的最优解和最优函数值,而这个过程可以通俗理解为“先进的、有目的的随机搜索”。用数学式子来表示就是:
这个过程会经历一些不断试错的过程,中途可能会产生许多“比较可能”是最优的解(即局部最优解);我们的算法要想方设法跳脱局部最优解,尽可能找到全局最优解。
故综合来看,数值最优化方法的理论有两个关键点:
1,按照一定的规则产生新的可行解x;产生的解x必须要先符合约束条件,再去研究它是否为最优解。
2,产生的新解x后要制定一套详细的规则决定是接受还是拒绝它。
因为当前的解 a 可能是局部最优解,使得新解 b有:f(b)<f(a);如果就此停止迭代,可能找到的就不是全局最优解(全局最大值)。这涉及到一个搜索策略的取舍问题:保守&冒险。保守的策略倾向于根据已知情况寻找最优解;比如我已经知道a附近的取值 会越来越大,那我就尽量在这附近搜索。冒险的策略则是更愿意去搜索之前没有探索过的区域,这更可能发现全局最优解,跳出局部最优解;但是消耗时间会更长。
编程上的两个关键点:
1、如何产生新解,很大程度上影响了最后找到的最优解的质量;
2,要明确目标函数和变量的关系,准确表述出来。
这里有一个编程小技巧,如果自己手写优化算法,可以将约束条件以惩罚函数的形式巧妙地融合在目标函数中。比如需要让 ,则目标函数可以写成:
,只要满足约束,惩罚项会无限小;否则,无限大。
智能算法本质上通过对动物群体行为的研究,将其抽象成寻找最优解的过程。整个过程又被称为“启发式搜索”,即在搜索最优解的过程中利用到了原来搜索过程中得到的信息,且这个信息会改进我们的搜索过程。它虽然不能保证能找到全局最优解,但是能更接近全局最优,且能加快求解过程。
核心思想是利用群体中的个体对信息的共享,使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的可行解。

这时,所有的鸟都会综合个体信息(自己所掌握的信息)和群体信息,对自己下一步的飞行速度做出决定:
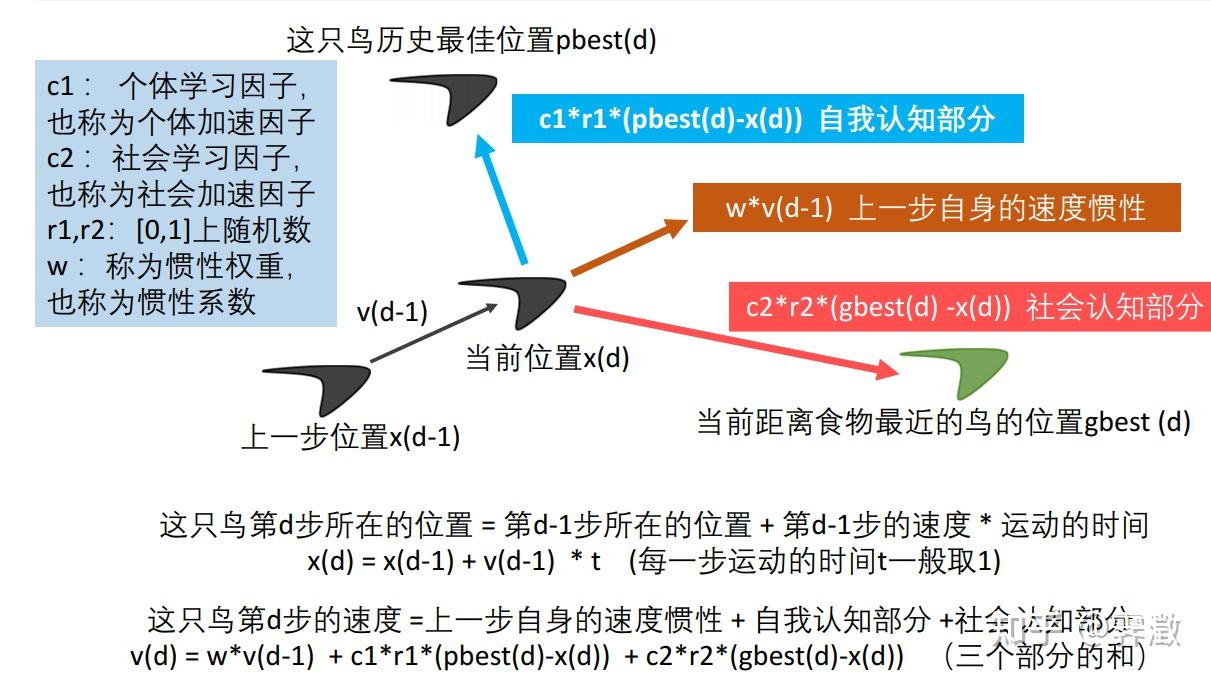
我们可以将这个过程和最优解的求解术语结合起来:
各个粒子就是优化问题的候选解(还要查看是否符合约束条件才能成为可行解),借助位置和速度的概念可以产生新的候选解;适应度(即函数最优解)评价粒子的优劣;而个体和群体分别有适应度;每一轮中,当个体的适应度优于前一轮的群体适应度,则当前轮次的适应度会被替换掉。
总结:粒子群算法中的多个粒子表明它每一次迭代同时产生了多个可行解供我们选择(类似于遗传算法,又不同于模拟退火算法),它是通过这种方式尽量避免陷入局部最优的。
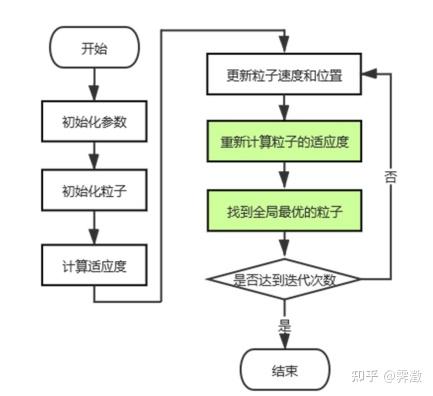
算法流程:
退火是一种金属热处理工艺,指的是将金属缓慢加热到一定温度,保持足够时间,然后以适宜速度冷却。
对于模拟退火算法,有两个关键点:
1、假设我们将搜索过程看作一个“工序”,那么搜索前期我们搜索的范围应该尽量大 ,搜索后期我们搜索的范围应该尽量小的 。
2、对于当前解a和找到的新解b,若f(b)<f(a),我们仍然要以一定概率接受它。
上面的两点是通过设置一个概率式子实现的:
可以看作一个和时间有关的系数,时间越长,它越大;因为我们希望前期搜索范围大,那么p应该大些,那么
应该小些;后期则相反。

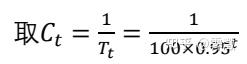
注意:不同于粒子群算法和遗传算法,模拟退火算法并没有给出产生新解的方法,我们需要自己根据情况设定。
算法流程:

例子:
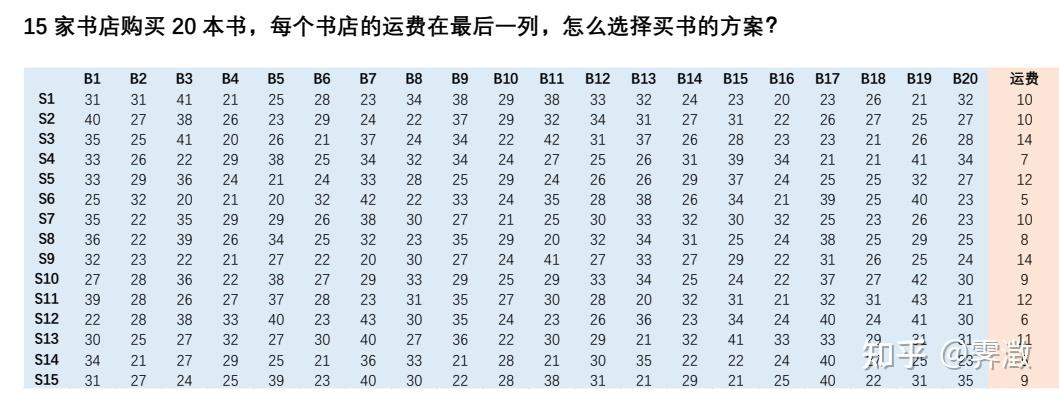
首先要明确目标函数:使得总费用最小,因此需要写一个计算费用的函数,其中solution是一个1x20的向量,每一个元素代表该书应该去哪家书店购买;book_price 和transportation 分别存储书费和运费。
function fee=Caculate_Fee(solution,book_price,transportation)
%book_price :15 stores x 20 books
store_index=unique(solution);
transportation_fee=sum(transportation(store_index));
book_fee=0;
for j=1:size(book_price,2)
book_fee=book_fee+book_price(solution(j),j);
end
fee=book_fee+transportation_fee;
end接着,需要一个产生新解的函数;这里产生新解主要有三种方法,比较好理解,但是效果不一定非常好;至于每种方法的使用概率,可以根据需要自己调:
%利用三种方式,根据当前解随机生成新解
function new_solution=GenerateNewSolution(old_solution,stores_num,books_num)
new_solution=old_solution;
%生成一个随机数决定用哪种生成方式
choose_way=unifrnd(0,1);
%生成一些随机数
index=randperm(books_num);
if choose_way<=1/15
index=sort(index(1:2));
%随机选择两个点交换位置
[location1,location2]=deal(index(1),index(2));
temp=new_solution(location1);
new_solution(location1)=new_solution(location2);
new_solution(location2)=temp;
elseif choose_way >(2/15) && choose_way <=(8/15)
index=sort(index(1:2));
%随机选择两个点,将这两点之间的顺序颠倒
[location1,location2]=deal(index(1),index(2));
slice=old_solution(location1:location2);
slice_back=slice(end:-1:1);
new_solution(location1:location2)=slice_back;
else
index=sort(index(1:3));
%随机选三个点,将前两个点之间的点移动到第三个点后
[location1,location2,location3]=deal(index(1),index(2),index(3));
slice=old_solution(location1:location2);
if location3 ~=books_num
slice2=old_solution(location3+1:end);
%删除
new_solution([location1:location2,location3+1:books_num])=[];
%重新拼接
new_solution=[new_solution,slice,slice2];
else
%删除
new_solution(location1:location2)=[];
%重新拼接
new_solution=[new_solution,slice];
end
end
end最后是主函数:
%模拟退火寻找最优买书方案
clear all;
data=xlsread("buying_books_opt.xlsx","B2:V16");
books_price=data(:,1:end-1);
transportation=data(:,end);
[stores_num,books_num]=size(books_price);
%参数初始化
T0=2500;%初始温度
max_iter=8000;%最大迭代次数
T=T0;%迭代时的温度
alpha=0.9;%温度衰减系数
T_iter=1800;%每个温度下的迭代次数
%随机生成一个初始解
solution0=randi(stores_num,[1,books_num]);
cost0=Caculate_Fee(solution0,books_price,transportation);
%保存中间过程的变量
min_cost=cost0;%当前最小值
cost_result=zeros(max_iter,1);%记录外层循环找到的Min_cost
solution_result=zeros(max_iter,books_num);
best_solution=solution0;
%模拟退火主过程
for iter=1:max_iter
for t=1:T_iter
NewSolution=GenerateNewSolution(solution0,stores_num,books_num);
NewCost=Caculate_Fee(NewSolution,books_price,transportation);
%如果新的花费更低,则更新;否则以一定概率更新
if NewCost < cost0
solution0=NewSolution;
cost0=NewCost;
else
p=exp(-(NewCost-cost0)/T);
if rand(1)<p
solution0=NewSolution;
cost0=NewCost;
end
end
%判断是否更新找到的最优解
if cost0< min_cost
min_cost=cost0;
best_solution=solution0;
end
end
cost_result(iter,1)=min_cost;
solution_result(iter,:)=best_solution;
T=alpha*T;
end
disp("最佳方案是去以下书店依次购买对应书籍:");disp(best_solution)
disp("花费最少:");disp(min_cost)过程涉及到的术语很多,不过大体思想还是大同小异。同粒子群算法一样,遗传算法每迭代一次会产生大量群体(染色体)供我们进行选择,通过这种方式来尽可能避免局部最优解;通过交配、变异等方式会产生新的可行解,这些可行解可能可以帮助我们跳出局部最优解。
遗传算法大致有如下5个步骤:

其中第一步对应算法的初始化,产生大量初始种群(初始可行解),一般来说,初始解的个数越多,越有可能找到最优解;而且在某些时候,给定的初始解相当重要,会直接影响优化的走向。(比如某些100个人里选10个人执行任务,解空间要求必须是10个1到100之间不重复的整数,某些package自己产生的解死活不满足这个要求,即使在目标函数里施加了一个无限大的惩罚)。
第二步对应算法的目标函数(需要最大化适应度函数值),根据不同的问题自定义即可。
第三四五步对应新解的产生和最优解的选择。
其中,需要在父辈中根据适应度选择优良的个体,然后进行杂交、变异产生新解。这一步也是需要根据问题类型进行自定义,产生新解的质量对最后最优解的过程也有很大影响。

在遗传算法中,群体对应候选解的集合,染色体对应每个群体中的候选解,基因对应每个解的维度。
两种产生新解的方式
crossover:

mutation:

下面用遗传算法解决著名的旅行商问题。该问题是一个商人需要依次访问120个城市,怎样访问总路径最短。我会就几个关键的步骤进行讲解。
首先,是对种群进行初始化。给出一些符合约束的初始解非常重要(特别是调包的时候),因为可以以此为基础进行更新迭代,否则很可能长时间都得不到符合约束的解:
function Chrom=InitPop(NIND,N)%innitialize the populations
%NIND: population size
%N: the length of chrome (city number or solution number)
Chrom=zeros(NIND,N);
for i=1:NIND
Chrom(i,:)=randperm(N);
end
end下一步是定义损失函数(适应度函数)。损失函数需要最小化,而适应度函数需要最大化。这主要由2个步骤组成:1,得出一个所有城市之间的距离矩阵;2,根据路线和距离矩阵,计算总距离。
计算总距离的函数:
function cost=total_dist(index,coordinate)
%coordinate : n cities x 2 coordinates (x y)
dist_mat=pdist2(coordinate,coordinate);
cost=0;
for i=1:length(index)-1
i1=index(i);
i2=index(i+1);
cost=cost+dist_mat(i1,i2);
end
cost=cost+dist_mat(index(1),index(end));
end适应度函数需要调整一下:
function objective=fitness(cost)
% in objective function we maximize the object
objective=1https://zhuanlan.zhihu.com/p/cost;
end另外,需要一个函数计算并储存种群中所有个体的总距离:
function len=PathLength(coordinate,Chrom)
%calculate the distance of all indivisulas
NIND=size(Chrom,1);
len=zeros(NIND,1);
for i=1:NIND
dist=total_dist(Chrom(i,:),coordinate);
len(i,1)=dist;
end第三步是从父代种群中根据适应度选择后续进行杂交、变异的个体(即优胜劣汰),这里我们选用轮盘赌法。
轮盘赌选择法又称比例选择方法.其基本思想是:各个个体被选中的概率与其适应度大小成正比.
具体操作如下:
(1)计算出群体中每个个体的适应度f(i=1,2,…,M),M为群体大小;
(2)计算出每个个体被遗传到下一代群体中的概率:
(3)计算出每个个体的累积概率;
(4)在[0,1]区间内产生一个均匀分布的伪随机数r;
(5)若r<q[1],则选择个体1,否则,选择个体k,使得:q[k-1]<r≤q[k]成立;
(6)重复(4)、(5)共M次
(具体可以参考文章轮盘赌选择法_如何根据适应度来概率选择_依萍如洗的博客-CSDN博客)
轮盘赌法选择一个个体的函数:
% SUS : select one based on the fitness of each individual
function select_one=SUS_one(fitness,r)
%fitness : n individual x 1
% r :a random number between[0,1]
p=fitnesshttps://zhuanlan.zhihu.com/p/sum(fitness);
m=0;
for i=1:length(fitness)
m=m+p(i);
if r<=m
select_one=i;
break;
end
end利用上述函数选择个NSel个体:
% select some indiviuals for next generation
function SelCh=Select(Chrom,FitnV,GGAP)
%Chrom population
%FitnV fitness value
%GGAP selection probability
NIND=size(Chrom,1);%population size
NSel=max(floor(NIND * GGAP+.5),2); % calculate seletion number
% save seletion index
ChrIx=[];
for i=1:NSel
% get a random number between[0,1]
r=rand();
select_id=SUS_one(FitnV,r);
ChrIx=[ChrIx;select_id];
SelCh=Chrom(ChrIx,:);
end
end第四步是利用选择的个体进行杂交:
注意,TSP问题中有一个很强的约束条件,即路线中不能有重复序号;但是两个个体一旦在某个片段交换后,一定会产生重复位点。举例如下:
个体1 : 1 2 3 4 5 个体2 : 2 3 4 1 5
假设在第二、三个位点之间进行交换,新片段:
个体1 : 1 3 4 4 5 个体2 : 2 2 3 1 5
此时的处理手法是:找出两个个体未交换片段中与交换片度的重复位点,进行交换:
个体1 : 13 4 4 5 个体2 : 2 2 3 1 5 变成:
个体1 : 13 4 2 5 个体2 : 4 2 3 1 5
交换函数如下:
function[a,b]=intercross(a,b)
%input: a and b needed to intercross
%output: a and b after intercross
L=length(a);
% generate intercross reigon by random
r1=randsrc(1,1,[1:L]);% a number between 1-L
r2=randsrc(1,1,[1:L]);
if r1~=r2
a0=a;
b0=b;
s=min([r1,r2]);
e=max([r1,r2]);
for i=s:e
a1=a;
b1=b;
% first interchange
a(i)=b0(i);
b(i)=a0(i);
% find same city in one chrome
x=find(a==a(i));
y=find(b==b(i));
% second exchange
i1=x(x~=i);
i2=y(y~=i);
if ~isempty(i1)
a(i1)=a1(i);
end
if ~isempty(i2)
b(i1)=b1(i);
end
end
end根据概率随机选择片段进行杂交的函数:
function SelCh=Recombin(SelCh,Pc)
%implement the intercross operation
%input: SelCh indivisuals seleted Pc: intercross probability
%output: SelCh indivisuals after intercross
NSel=size(SelCh,1);
for i=1:2:NSel - mod(NSel,2)
if Pc>=rand
[SelCh(i,:),SelCh(i+1,:)]=intercross(SelCh(i,:),SelCh(i+1,:));
end
end还有突变的函数,根据概率随机选择一些片段进行倒序:
function SelCh=Mutate(SelCh,Pm)
%Pm mutation probability
[NSel,L]=size(SelCh);
for i=1:NSel
if Pm >=rand
R=randperm(L);
SelCh(i,R(1:2))=SelCh(i,R(2:-1:1));
end
end最后是主函数,coordinate 表示城市座标:
NIND=100; %population size
MAXGEN=3000; % max iteration
Pc=0.9; % crossover p
Pm=0.05; % mutation p
GGAP=0.9; %generation gap,next generation number=parent generation num*GGAP
N=size(coordinate,1); % city num
%%innitilize popilation
Chrom=InitPop(NIND,N);
gen=0;
figure;
hold on;
box on;
xlim([0,MAXGEN])
title('update process')
xlabel('iteration')
ylabel('curent optimal')
%current distnace
ObjV=PathLength(coordinate,Chrom);
preObjV=min(ObjV);
while gen<MAXGEN
%%calculate fitness
ObjV=PathLength(coordinate,Chrom);
line([gen - 1,gen],[preObjV,min(ObjV)]);
pause(0.0001);
preObjV=min(ObjV);
FitnV=fitness(ObjV);
%selection
SelCh=Select(Chrom,FitnV,GGAP);
%cross over
SelCH=Recombin(SelCh,Pc);
%mutation
SelCh=Mutate(SelCh,Pm);
%reverse
SelCh=Reverse(SelCh,coordinate);
%new population
Chrom=Reins(Chrom,SelCh,ObjV);
% update iteration
gen=gen + 1;
end
%best solution
ObjV=PathLength(coordinate,Chrom);
[minObjV,minInd]=min(ObjV);
best_path=Chrom(minInd(1),:);
for i=1:length(best_path)-1
i1=best_path(i);
i2=best_path(i+1);
coor1=coordinate(i1,:);
coor2=coordinate(i2,:);
x1=coor1(1);
y1=coor1(2);
x2=coor2(1);
y2=coor2(2);
plot([x1,x2],[y1,y2]);
hold on;
end
i1=best_path(1);
i2=best_path(end);
coor1=coordinate(i1,:);
coor2=coordinate(i2,:);
x1=coor1(1);
y1=coor1(2);
x2=coor2(1);
y2=coor2(2);
plot([x1,x2],[y1,y2]);所有代码在这:
https://github.com/ZeonlungPun/Numeric-Optimization/tree/main/genetic-algorithmmatlab内置了很多智能算法的函数,我们直接调用即可。
1,粒子群算法:[index1,fval1]=particleswarm(obj_fun,narvs,lb,ub,options);
其中index1为返回的最优解X,fval1为找到的最优值;obj_fun为需要优化的目标函数,narvs:要优化的变量数量;lb、ub:X的边界约束。
2,遗传算法:[index2,fval2]=ga(obj_fun,narvs,A,b,Aeq,beq,lb,ub);
不等式约束:A*x<=b ;等式约束:Aeq*x=beq
3,模拟退火算法:[index3,fval3]=simulannealbnd(obj_fun,x0,lb,ub);
x0:初始值
先设定好目标函数:(我直接用每个算法跑出了300个解,然后存储起来找最好的解)
function cost=cal_fee(store_index,data)
store_index=round(store_index);
book_price=data(:,1:end-1);
transportation=data(:,end);
book_cost=0;
for i=1:length(store_index)
book_cost=book_cost+book_price(store_index(i),i);
end
store=unique(store_index);
transportation_cost=sum(transportation(store));
cost=book_cost+transportation_cost;
end随后是一些基础设置:注意obj_fun要写成函数句柄的形式,@后面放的是需要优化的变量
narvs=20;
lb=ones(1,20);
ub=15*ones(1,20);
data=xlsread("buying_books_opt.xlsx","B2:V16");
obj_fun=@(store_index) cal_fee(store_index,data);主函数:
options=optimoptions("particleswarm","HybridFcn",@fmincon);
obj_array1=[];
input_array1=[];
obj_array2=[];
input_array2=[];
obj_array3=[];
input_array3=[];
times=300
for time=1:times
%初始值
if time==1
x0=randi(20,[1,20]);
else
x0=index3;
end
%粒子群算法
[index1,fval1]=particleswarm(obj_fun,narvs,lb,ub,options);
%遗传算法
[index2,fval2]=ga(obj_fun,narvs,[],[],[],[],lb,ub);
%模拟退火
[index3,fval3]=simulannealbnd(obj_fun,x0,lb,ub);
input_array1(time,:)=index1;
input_array2(time,:)=index2;
obj_array1(time)=fval1;
obj_array2(time)=fval2;
input_array3(time,:)=index3;
obj_array3(time)=fval3;
end
min(obj_array1)
min(obj_array2)
min(obj_array3)
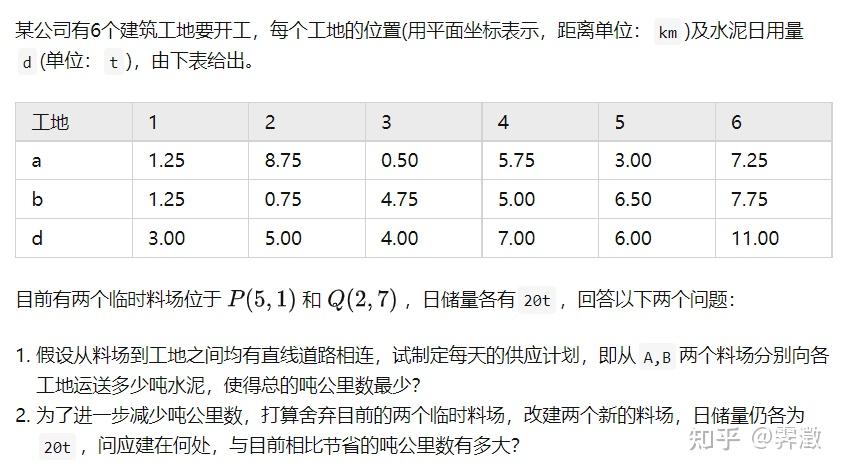
第一问比较简单,主要算出分别向每个工地运输多少水泥即可:
计算距离的函数:
%c_ij i=1,2 j=1,2,^,6 从i料场向j工地运输c_ij吨水泥
%c=[c11,c12,^,c16,c21,^c26]
function cost=cal_dist(c)
%保留三位小数,精确到KG
c=roundn(c,-2);
c=reshape(c,6,2)';
location1=[1.25,1.25;8.75,0.75;0.5,4.75;5.75,5;3,6.5;7.25,7.75];
location2=[5,1;2,7];
[minus1,minus2]=deal(location1-location2(1,:),location1-location2(2,:));
%到第一个料场的距离
dist1=bsxfun(@hypot,minus1(:,1),minus1(:,2));
%到第二个料场的距离
dist2=bsxfun(@hypot,minus2(:,1),minus2(:,2));
%从P运输水泥的总距离
Pdist=c(1,:)*dist1;
%从Q
Qdist=c(2,:)*dist2;
total_dist=Pdist+Qdist;
cost=total_dist;
end
主函数:(注意约束函数的书写,最好在草稿纸上写成矩阵的形式,不然很容易出错)
%c_ij i=1,2 j=1,2,^,6 从i料场向j工地运输c_ij吨水泥
%c=[c11,c12,^,c16,c21,^c26]
function cost=cal_dist(c)
%保留三位小数,精确到KG
c=roundn(c,-2);
c=reshape(c,6,2)';
location1=[1.25,1.25;8.75,0.75;0.5,4.75;5.75,5;3,6.5;7.25,7.75];
location2=[5,1;2,7];
[minus1,minus2]=deal(location1-location2(1,:),location1-location2(2,:));
%到第一个料场的距离
dist1=bsxfun(@hypot,minus1(:,1),minus1(:,2));
%到第二个料场的距离
dist2=bsxfun(@hypot,minus2(:,1),minus2(:,2));
%从P运输水泥的总距离
Pdist=c(1,:)*dist1;
%从Q
Qdist=c(2,:)*dist2;
total_dist=Pdist+Qdist;
cost=total_dist;
end
第二问:
计算距离的函数:
%c_ij i=1,2 j=1,2,^,6 从i料场向j工地运输c_ij吨水泥
%最后两个参数是供应商坐标
%var=[c11 c12 c13,^,c25,c26,x1,y1,x2,y2]
function cost=cal_dist3(var)
%保留三位小数,精确到KG
var=roundn(var,-2);
location2=var(end-3:end);
location2=reshape(location2,2,2);%注意reshape后形式的排布
location2=location2';
c=var(1:end-4);
c=reshape(c,6,2);
c=c';%(2,6)
location1=[1.25,1.25;8.75,0.75;0.5,4.75;5.75,5;3,6.5;7.25,7.75];
[minus1,minus2]=deal(location1-location2(1,:),location1-location2(2,:));
%到第一个料场的距离
dist1=bsxfun(@hypot,minus1(:,1),minus1(:,2));
%到第二个料场的距离
dist2=bsxfun(@hypot,minus2(:,1),minus2(:,2));
%从P运输水泥的总距离
Pdist=c(1,:)*dist1;
%从Q
Qdist=c(2,:)*dist2;
total_dist=Pdist+Qdist;
cost=total_dist;
end主函数:
%运输水泥成本计算
%加选最优场地
narvs=16;
lb=zeros(1,16);
ub=20*ones(1,16);
obj_fun=@(c) cal_dist3(c);
options=optimoptions("ga","HybridFcn",@fmincon,"PopulationSize",200);
A=[ones(1,6),zeros(1,10) ;zeros(1,6),ones(1,6),zeros(1,4)];
supply=[20;20];
Aeq=[eye(6),eye(6),zeros(6,4)];
demand=[3 5 4 7 6 11]';
c_array1=[];
times=5;
cost_array1=zeros(times,16);
for i=1:times
[c_min,fval]=ga(obj_fun,narvs,A,supply,Aeq,demand,lb,ub,[],[],options);
c_array1(i)=fval;
cost_array1(i,:)=c_min;
end
min(c_array1)
[min_num,min_index]=min(c_array1);
input=cost_array1(min_index,:);
input=roundn(input,-2);
loc=input(end-3:end);
loc=reshape(loc,2,2)';
c=input(1:end-4);
c=reshape(c,6,2)';
constrain1=sum(c,2)-supply;
constrain2=sum(c,1)-demand';
judge1=(constrain1<=20);
judge2=(constrain2==0);近年来,深度学习愈发火爆,让其在各领域的应用越来越广;但是,深度学习模型的超参数非常的多,让我们在设置和应用模型时困难重重。因此,AutoML提出了一种方便我们调参的贝叶斯优化算法。
同样道理,我们可以将所有超参数当成输入变量X,需要优化的变量比如模型准确率、模型错选率当做模型的输出Y,我们假设超参数和需要优化的变量之间有一个隐含的、确定的函数关系: ;贝叶斯优化利用高斯过程回归的方法根据选取的不同超参数和模型输出结果拟合出一个近似的函数:
,希望随着采样的不断增多,
能趋近于
。至于如何采样,贝叶斯优化算法有很多配套的方法,这些方法称作acquisition function。其实贝叶斯优化方法本质上和智能算法的思想十分相近,都是一种“启发式优化”的思想,只不过它被更专注于应用在机器学习的调参领域,希望选择一些最优超参数,使得模型表现最好。
下面的内容是我总结这两篇博文再加上自己的理解而来:
代忠祥:贝叶斯优化/Bayesian Optimization假设我们需要优化的函数是 ,需要解决的优化问题可以表述为:
。
假设我们利用贝叶斯优化算法迭代T次得到最终结果,而在第t次( )次时,我们选择一个输入
,同时得到对应的观测值
,
与
对应的真值
之间存在着一定的差异:
,其中
是高斯噪声。我们把新观测到的这组值
加到我们所有的观测到的数据里面,然后进行下一个迭代t+1。
这里便是贝叶斯优化思想的体现了:由于我们要优化的这个函数 不可能求解,要想得到
对应的观测值
,一个自然的想法就是用一个简单点的模型
来近似
,这个替代原始函数的模型也叫做代理模型,贝叶斯优化中的代理模型为“高斯过程回归”模型。假设我们对待优化函数的先验(prior)为高斯过程(即把分布的概念由随机变量推广到函数中,假定函数也服从某个分布:
),经过一定的试验我们有了数据
(也就是evidence),然后根据贝叶斯定理就可以得到这个函数的后验分布(第t+1次迭代时f(x)的预测分布):
;有了这个后验分布后,我们需要考虑下一次试验点在哪里进一步收集数据,因此就会需要构造一个acquisition函数用于指导搜索方向(选择下一个试验点),然后再去进行试验,得到数据后更新代理模型的后验分布,反复进行。
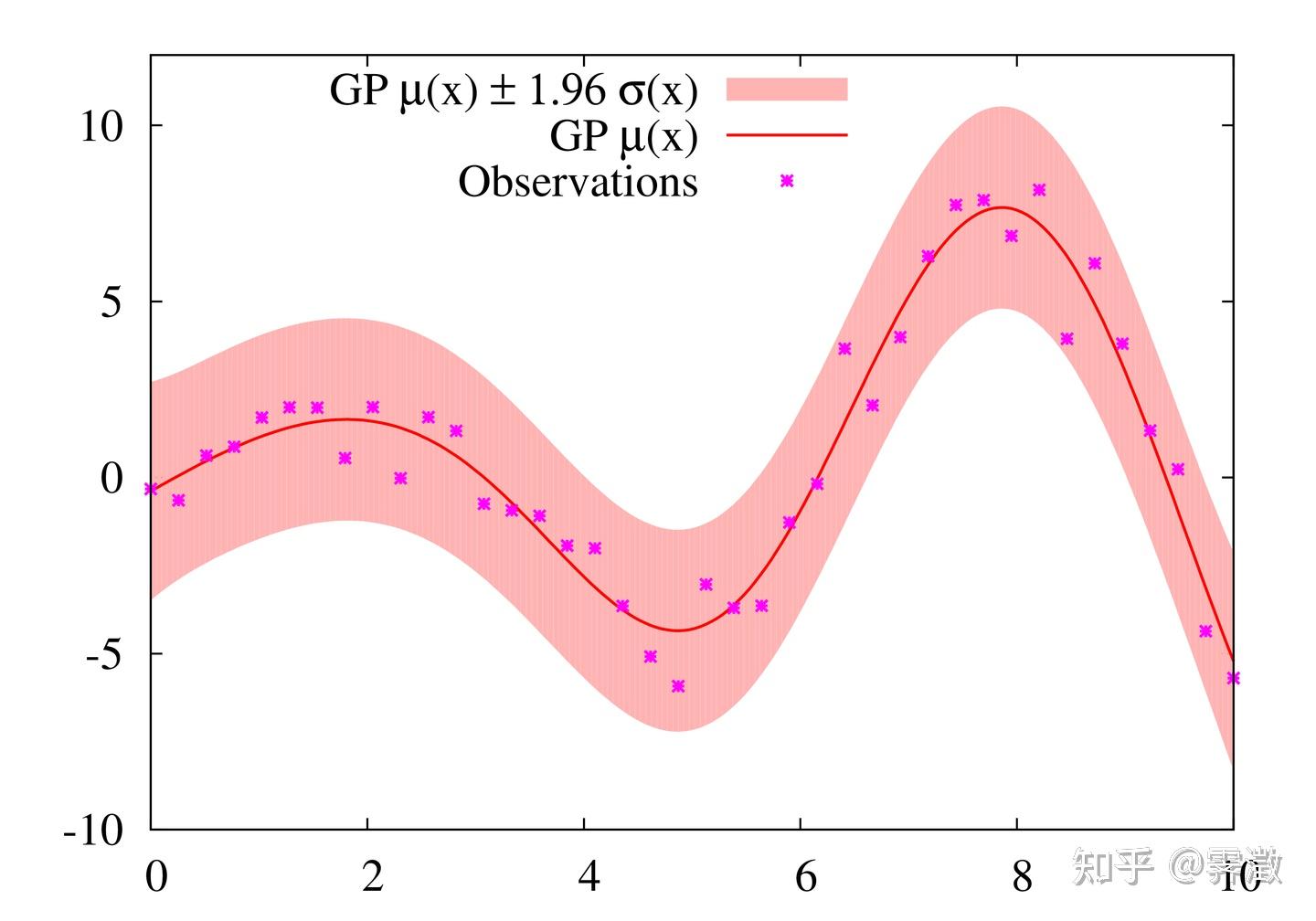
上图蓝色是观测点,红线便是由观测逼近的预测分布。
现在,贝叶斯优化问题的核心便转变为在每一次迭代中,如何采样新的观测点: ,也就是:
。实质上在这里,我们利用acquisition function把一个优化问题替换成了好多个优化问题。所以这个acquisition function需要有几个要求:第一,必须优化起来非常容易;第二,设计该acquisition function时必须做好exploration-exploitation trade-off,即在选下一个点
的时候,我们既想要去尝试那些我们之前没有尝试过的区域的点(exploration),又想要去选择根据我们目前已经观测到的所有点预测的
的值比较大的点(exploitation)。exploration是为了尽可能跳出局部最优点从而找到可能的全局最优点,exploitation是为了保证在当前能够得到一个较为优异的结果,找到附近的局部最优点。为了能很好地平衡这两点,对于domain
里面任意一个点
,我们既需要预测对应的
的值(为了exploitation),又需要知道对应的
的uncertainty(为了exploration)。然后利用预测的这两个值构造acquisition function进行采样。故
的代理函数
最适合的是“高斯过程回归”模型。
1, 最大化提升概率 probability of improvement (PI)
最容易想到的就是希望下一次试验的结果比当前所有观测结果都要好( ),或者说这个新采样的函数值更优的概率要大
但是光这样考虑是有点目光短浅的,它忽略了对不确定性的考虑,一味追求选择大概率肯定大于 的点,也就是一直在exploitation,这样的缺点是可能就陷入了局部最优,忽略了潜在的全局最优解。改进的方法也很简单,加个偏置就可以了:
为超参数,可以指导模型去更多的探索(exploration),也就可能获得更优的解。
2,最大化提升量 Expected Improvement (EI)
提升的概率大并不意味着提升得多,一种量化的角度就是考虑提升量(可以不严谨地理解为梯度下降法中,不仅要下降,而且要下得更多一点)。EI[2]的假设是没有observation noise,也就是我们每一个iteration都可以直接观察到 ,而不是
。首先定义
,也就是
是前
次迭代里面我们观察到的最大值。
EI策略定义为
其中 和
分别是standard Gaussian distribution的cumulative distribution function(CDF)和probability density function(PDF)。注意第一行里面的expectation是对于
的posterior distribution的,这个在之前讲GP的时候有提到,他的distribution是一个一维高斯分布:
。
推导过程如下:
令 且有 :
,
而根据重参数技巧(reparameterization trick), ,
(下面为了方便省略部分上下标);
所以,根据期望的定义:
when , 我们可以推出:
故
=
对于后面一项:
=
推导完毕。
3, 最大化置信上界 Gaussian Process-Upper Confidence Bound (GP-UCB)
由于我们的代理模型是高斯过程,预测为分布,即有均值也有方差,那么就可以构造一个置信上界
这样的上界同时考虑了预测值的大小以及不确定性,高斯过程在观测数据的位置不确定性(方差)小,在未探索区域的不确定大。 在实际应用中设成一个常数,用以平衡预测值的大小以及不确定性。
贝叶斯优化伪代码
1,定义高斯过程
from sklearn.gaussian_process import GaussianProcessRegressor
self.GP=GaussianProcessRegressor(...)2,定义acquisition function
def PI(x, gp, y_max, xi):
mean, std=gp.predict(x, return_std=True)
z=(mean - y_max - xi)/std
return norm.cdf(z)
def EI(x, gp, y_max, xi):
mean, std=gp.predict(x, return_std=True)
a=(mean - y_max - xi)
z=a / std
return a * norm.cdf(z) + std * norm.pdf(z)
def UCB(x, gp, kappa):
mean, std=gp.predict(x, return_std=True)
return mean + kappa * std3,寻找acquisition function最大的对应解
def acq_max(ac, gp, y_max, bounds, random_state, n_warmup=10000):
# 随机采样选择最大值
x_tries=np.random.RandomState(random_state).uniform(bounds[:, 0], bounds[:, 1],
size=(n_warmup, bounds.shape[0]))
ys=ac(x_tries, gp=gp, y_max=y_max)
x_max=x_tries[ys.argmax()]
max_acq=ys.max()
return x_max
4,主函数
while iteration < n_iter:
# 更新高斯过程的后验分布
self.GP.fit(X, y)
# 根据acquisition函数计算下一个试验点
suggestion=acq_max(
ac=utility_function,
gp=self.GP,
y_max=y.max(),
bounds=self.bounds,
random_state=self.random_state
)
# 进行试验(采样),更新观测点集合
X.append(suggestion)
y.append(target_func(suggestion))
iteration +=1
我们希望神经网络做回归任务,需要选择一些超参数,使得预测结果和真实结果的R-squre最小
from bayes_opt import BayesianOptimization
import tensorflow as tf
def nn_model(l1_rate,l2_rate,dropout_rate):
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(100, activation='relu', input_shape=x_train.shape[1:]),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(100, activation='relu',kernel_regularizer=tf.keras.regularizers.l1_l2(l1=l1_rate,l2=l2_rate) ),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(dropout_rate),
tf.keras.layers.Dense(80, activation='relu', kernel_regularizer=tf.keras.regularizers.l1_l2(l1=l1_rate,l2=l2_rate)),
tf.keras.layers.Dropout(dropout_rate),
tf.keras.layers.Dense(50, activation='relu', ),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dense(y_train.shape[1], activation='sigmoid'),
])
return model
def black_box_function(batch_size,lr,epochs,l1_rate,l2_rate,dropout_rate):
model=nn_model(l1_rate=l1_rate,l2_rate=l2_rate,dropout_rate=dropout_rate)
opt = tf.keras.optimizers.Adagrad(learning_rate=lr)
model.compile(loss=customed_mse,metrics=customed_mse,optimizer=opt)
history = model.fit(x_train_scaled,y_train_scaled, shuffle=False, workers=1,
validation_data=(x_val_scaled, y_val_scaled),verbose=False,
epochs=round(epochs), batch_size=round(batch_size))
pred=model.predict(x_val_scaled)
score=adjusted_r2score(y_val,pred,y_val_scaled)
score_sort=np.sort(np.array(score))
return score_sort[0]+score_sort[1]+score_sort[2]
# 贝叶斯优化调参
optimizer = BayesianOptimization(f=black_box_function, pbounds=pbounds, verbose=2, random_state=1)
optimizer.maximize(n_iter=30)
print(optimizer.max)
# 预测,用最好的参数再次构建模型
epochs = round(optimizer.max['params']['epochs'])
batch_size = round(optimizer.max['params']['batch_size'])
lr = optimizer.max['params']['lr']
l1_rate=optimizer.max['params']['l1_rate']
l2_rate=optimizer.max['params']['l2_rate']
dropout_rate=optimizer.max['params']['dropout_rate']
opt = tf.keras.optimizers.Adagrad(learning_rate=lr)
model1=nn_model(l1_rate=l1_rate,l2_rate=l2_rate,dropout_rate=dropout_rate)
model1.compile(loss=customed_mse, metrics=customed_mse, optimizer=opt)
history = model1.fit(x_train_scaled, y_train_scaled, shuffle=False, workers=1,
validation_data=(x_val_scaled, y_val_scaled), verbose=False,
epochs=round(epochs), batch_size=round(batch_size))
pred1 = model1.predict(x_train_scaled)
pred2 = model1.predict(x_test_scaled)
如有需求请您联系我们!
地址:海南省海口市58号
电话:18888889999
手机:海南省海口市58号
Copyright © 2012-2018 首页-杏彩体育中国官方网站 版权所有 ICP备案编:琼ICP备88889999号
