深度学习中的优化器的思想来源基本上都是梯度下降(Gradient Descent)

根据以上框架，我们来分析和比较梯度下降的各种变种算法。
Vanilla SGD(朴素SGD)
朴素SGD最为简单且没有动量的概念。

注意这里的I2是指单位矩阵的平方。
SGD的缺点在于收敛速度慢，可能在鞍点处震荡，并且如何选择学习率是SGD的一大难点。

Momentum(动量法)
SGD在遇到沟壑时容易陷入震荡。为此可以为其引入动量(Momentum),加速SGD在正确的方向下降并抑制震荡。

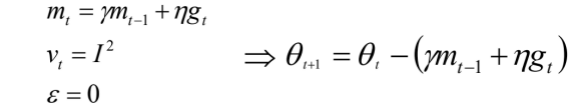
SGD-M在原步长的基础上，增加了与上一个时刻步长相关的γmt-1,γ通常取0.9左右。
这意味着参数更新方向不仅由当前的梯度决定，也与此前累积的下降方向有关。这使得参数中那些梯度方向变化不大的维度可以加速更新，并减少梯度方向变化较大的维度上的更新幅度。由此产生了加速收敛和减小震荡的效果。

从上图可以看出，引入动量有效的加速了梯度下降的收敛过程。

Nesterov Accelerated Gradient(牛顿加速梯度，也称牛顿动量法)
更进一步的，人们希望下降的过程更加智能：算法能够在目标函数有增高趋势之前，减缓更新速率。NAG就是为此而设计的，其在SGD-M的基础上进一步改进了步骤一中的梯度计算公式：

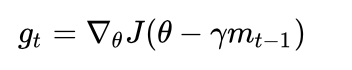
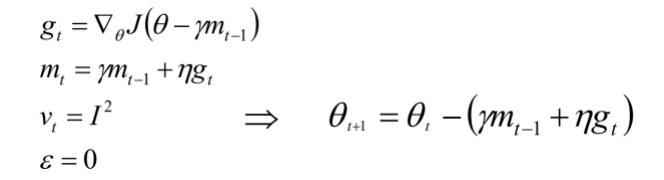
参考图二，SGD-M的步长计算了当前梯度(短蓝向量ηgt)和动量项(长蓝向量γmt-1)。然而，既然已经利用了动量项来更新，不妨先计算出下一时刻θ的近似向量(棕向量,(θ-γmt-1))，并根据该未来位置计算梯度(红向量，新的gt)，然后使用和SGD-M中相同的方式计算步长(绿向量(γmt-1+ηgt))。这种计算梯度的方式可以使算法更好的预测未来，提前调整更新速率。
注意：由于J(θ)是当前的目标函数，而J(θ-γmt-1)则就是下一时刻的目标函数了。

Adagrad
SGD,SGD-M和NAG均是以相同的学习率去更新θ的各个分量。但是深度学习模型中往往涉及大量的参数，不同参数的更新频率往往有所区别。对于更新不频繁的参数(典型例子:更新word embedding中的低频词)，我们希望单次步长更大，多学习一些知识；对于更新频繁的参数，我们希望步长较小，使得学习到的参数更稳定，不至于被单个样本影响太多。
Adagrad算法为了达到此效果，引入了二阶动量(diag意为取矩阵对角线上的值)：

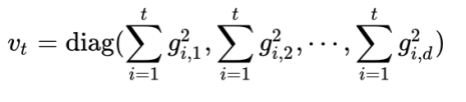
其中，vt是对角矩阵，其元素vt,i为参数第i维从初始时刻到时刻t的梯度平方。
此时可以这样理解：学习率等价为ηt+?）。对于此前频繁更新的参数，其二阶动量对应的分量较大，导致学习率较小；而对于更新不频繁的参数则对应的学习率较大。

RMSprop
在Adagrad中，vt是单调递增的，使得学习率逐渐递减至0，可能导致训练提前结束。为了改进这一缺点，可以考虑在计算二阶动量时不累积全部历史梯度，而只关注最近某一时间窗口内的下降梯度，据此思想有了RMSprop。记

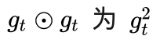
有：

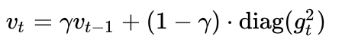
其二阶动量采用指数移动平均公式计算，这样可以避免二阶动量持续累积的问题。使用γ衰减系数来控制对于历史动量的引入大小，一般建议值为0.9左右。

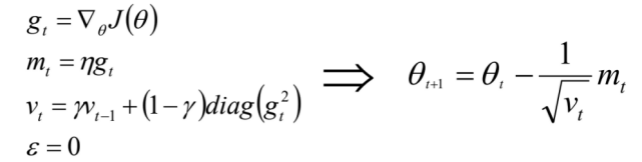
Adam
Adam可以认为是RMSprop和Momentum的结合。和RMSprop对二阶动量使用指数平均类似，Adam中对一阶动量也是用指数移动平均来计算的。

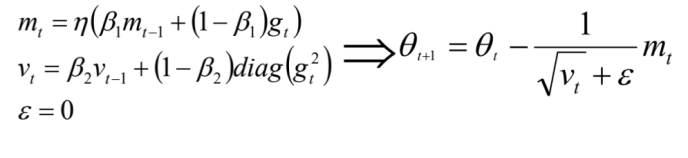
参考文章：
1一个框架看懂优化算法之异同 SGD/AdaGrad/Adam
2从 SGD 到 Adam —— 深度学习优化算法概览(一)